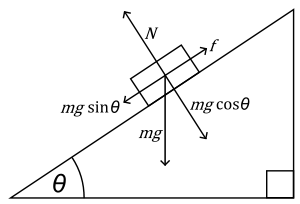
Friction on an inclined plane

Consider a mass m lying on an inclined plane, If the direction of motion of the mass is down the plane, then the frictional force F will act up the plane. This can be seen in the image below.

N = normal force exerted on the body by the plane due to the force of gravity i.e. mg cos θ f = frictional force mg = mass x gravity

The weight of the mass is mg and this will cause another 2 forces to act on itself, these being N and mg sin θ.

Forces up the plane = Forces down the plane
(f = mg sin θ)

Forces up = forces down
(N = mg cos θ)

If we divide the 2 equations above we get:

But therefore tan θ = µ

µ = The coefficient of friction

By gradually increasing θ until the mass begins motion then value of θ will be called the limiting angle of repose, with this you can obtain the maximum value of µ for static friction.

<<Back